> restart;

Несмотря на достоинства описанного выше метода повторяющегося деления, он может Вам показаться слишком медленным (особенно когда Вы пытаетесь достигнуть высокой степени точности результата), особенно при выполнении всех описанных действий вручную. Если нам известно, что функция не только непрерывна, но и дифференцируема, то можно воспользоваться идеей линейного приближения. Из предлагаемого ниже рисунка следует: определив каким-то образом достаточно узкий диапазон, которому принадлежит корень функции , в качестве приближения корня можно выбрать абсциссу точки пересечения касательной, проведенной к графику функции в какой-то "стартовой" точке. (На рисунке у такой начальной точки .)

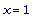> f := x -> x^2 - 2;

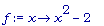
> x0 := 1;

> t1 := x -> f(x0) + D(f)(x0)*(x-x0);

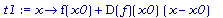
> plot({f,t1}, 0..3);

Теперь, разумеется, мы "зациклим" наши действия и найдём точку, в которой касательная пересекает ось . Теперь уже эта точка станет новым приближенным значением корня. И уже касательную к графику функции мы проведём в точке графика именно с этой новой абсциссой. И вновь будем интересоваться точкой пересечения касательной с осью . Описанную процедуру будем повторять до тех пор, пока не получим достаточно точное значение корня функции.

> x1 := solve(t1(x) = 0, x);

> t2 := x -> f(x1) + D(f)(x1)*(x-x1);

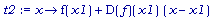
> plot({f,t2}, 0..3);

Обратите внимание: уже после первой итерации нам придётся "вооружиться микроскопом", чтобы увидеть на рисунке различие между истинным корнем функции и точкой пересечения касательной с осью .

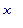> x2 := solve(t2(x) = 0, x); evalf(%);

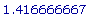
"Всё опять повторится сначала!":

> t3 := x -> f(x2) + D(f)(x2)*(x - x2);

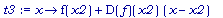
> x3 := solve(t3(x) = 0, x); evalf(%);

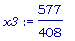
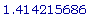
Для сравнения, приведём значение , найденное Maple с точностью до 10 цифр :

> evalf(sqrt(2));

Очевидно, метод Ньютона гораздо быстрее (по крайней мере - для выбранного нами случая).