Идея метода повторного деления очень проста: если непрерывная функция где-то положительна, а где-то - отрицательна, то обязательно найдётся точка, в которой функция обращается в ноль. Традиционно, в качестве первого примера применения метода, рассматривают вычисляют приближенное значение 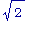, решая уравнение

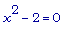
> restart;

> f := x -> x^2 - 2;

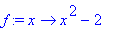
> plot(f, 0..4);

Как ясно видно из приведенного рисунка, функция обращается в 0 где-то на интервале (1,2). Довольно просто найти значения функции в этих граничных точках:

> f(1); f(2);

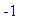
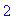
Функция меняет свой знак на интервале [1,2]; она имеет форму полинома, а значит - непрерывна, и, как следствие, обязана иметь корень на промежутке (1,2). Разумеется, теперь значение корня можно уточнять, с каждым разом сужая интервалы поиска. Весь фокус в том, каким методом следует вооружиться, чтобы достигнуть результата требуемой точности и за минимальное время. Один из самых замечательных приёмов состоит в повторяющемся делении пополам интервала, которому принадлежит корень, с одновременным вычислением значения функции в точке деления. При этом корень оказывается в одном из образовавшихся полуинтервалов, а точность ответа, условно говоря, повышается вдвое. Этот процесс можно повторять до тех пор, пока не будет достигнута требуемая точность при вычислении значения корня.

> m1 := (1 +2)/2; f(m1);

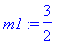
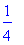
Искомое расположено на полуинтервале между 1 и 3/2, т.к. мы знаем, что 1 < 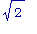< 1.5 . Повторим процедуру, но уже для интервала [1, 3/2].

> m2 := (1 + m1)/2; f(m2);

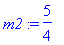
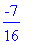
> m3 := (m2 + m1)/2; f(m3);

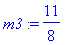
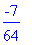
> m4 := (m3 + m1)/2; f(m4);

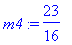
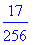
> evalf([m3,m4]);

> m5 := (m3 + m4)/2; f(m5);

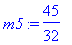
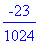
> m6 := (m5 + m4)/2; f(m6);

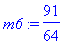
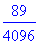
> evalf([m5,m6]);

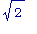Т.е. меняет свой знак на интервале [m5, m6], являясь при этом непрерывной, мы теперь знаем, что = 1.4 с точностью до второй значащей цифры.

(Гарантировано!) Может показаться, что мы проделали огромный объм работы, а получили столь незначительный результат. Однако следует помнить:

1) Мы иллюстрируем очень общий метод, который прекрасно зарекомендовал и в случаях более сложных уравнений.

2) В принципе, метод позволяет получить результат с любой степенью точности.

3) Наиболее важно то, что точность гарантирована : мы не только всё точнее определяем корень, но параллельно и сужаем интервал поисков. Корень при этом гарантированно попадает в новый, всё меньший по размерам интервал.

Конечно, Вы не могли не заметить, что метод навевает скуку своим однообразием. Это явный признак того, что он - подходящий кандидат для программирования. Предлагаем Вашему вниманию далёкую от идеала программу, которая для заданной функции и начального интервала выясняет, меняет ли на нём функция свой знак, а затем выполняет 10 подобных итераций.

> bisect10 := proc(f,a,b) local a1,b1,m,j:

> if (evalf(f(a)*f(b)) >= 0) then

> RETURN(`Изменения знака нет на интервале ` (a,b)):

> else

> a1 := a: b1 := b:

> for j from 1 to 10 do

> m := (a1 + b1)/2:

> if (f(a1)*f(m) < 0) then b1 := m:

> else a1 := m:

> fi:

> od:

> fi:

> print(`Имеется 0 в промежутке ` (evalf(a1), evalf(b1)) ):

> end:

> bisect10(f,2,3);

> bisect10(f,1,2);

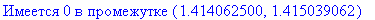
Вы можете объяснить следующий результат?

> bisect10(sin,-1,4);