На рисунке изображен сектор круга с центральным углом .

Пустьt A = A(theta) - площадь сегмента, ограниченного хородой PR и дугой PR.

Пустьt B = B(theta) - площадь треугольника PQR.

Найти правосторонний предел . Построить график отношения для придания наглядности Вашему ответу.

Предлагаем программу для графика.

> data:= ([0,0], [0.5, sqrt(3)/2]):

> data1:= ([0.5, sqrt(3)/2], [1,0]):

> data2:= ([0.5,sqrt(3)/2], [0.5,0]):

> a:= plot( sqrt(1 - x^2), x = 0..1, color = red):

> b:= plot([data], color = orange):

> c:= plot([data1], color = orange):

> d:= plot([data2], color = orange):

> e:= textplot([.07,.05,`O`],color = magenta):

> f:= textplot([.54,.05,`Q`], color = magenta):

> g:= textplot([.9,.05,`R`], color = magenta):

> h:= textplot([.4,.8,`P`], color = magenta):

> l:= textplot([.25,.15,`theta`], color = magenta):

> m:= textplot([.65,.35,`B`], color = red):

> n:= textplot([.8,.5,`A`], color = red):

> o:= plot(sqrt(.04 - x^2), x = 0.1..0.2, color = red):

> display(a,b,c,d,e,f,g,h,l,m,n,o, scaling=constrained);

Пусть радиус круга равен r. Имеем:

= площадь сектора - площадь треугольника OPR =

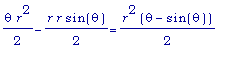
и

= |QR| |PQ|/2 = .

Следовательно,

=

=

=

= .

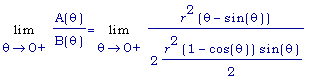
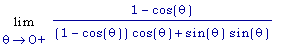
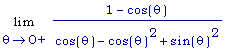
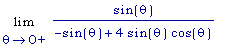
> A:= x -> (0.5) * x^2 * ( x - sin(x));

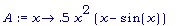
> B:= x -> (0.5) * x * ( 1 - cos(x)) * x * sin(x);

> az:=plot(A(x)/B(x), x = 0.01..Pi/2, color = red):

> bz:= plot([x,1/3, x = 0.01..Pi/2], color = magenta):

> display((az,bz));

> evalf( A(Pi/2) / B(Pi/2) );