Полониум-214 обладает временем полураспада 1.4 x секунд.

a) В предположении, что начальная масса составляет 50 мг, найти формулу для оставшейся массы через t секунд.

b) Как много времени пройдёт, пока масса полония не составит 40 мг?

Имеем:

25 = 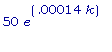=> => 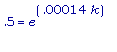ln(.5) = .00014k.

Следовательно,

.

> k:= ln(.5)/(.00014);

a) Искомая формула: y = 50*e^( 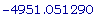*t)

b) Решим уравнение: 40 = 50*e^( *t) . Следовательно,

t = ln(4/5) / ( ).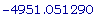

> evalf(ln(4/5) / (-4951.051290));

Понадобится всего лишь секунд для того, чтобы от куска осталось 40 мг.

> f2:= t -> 50 * e^(-4951.051290 * t);

> plot(f2(t), t = 0..5);

> evalf(e^(-4951.051290));

График функции f2 при опциях, заданных по умолчанию, не получился, т.к. функция очень быстро убывает. Но Вы можете всё-таки его построить, задав диапазон изменения переменных (и прежде всего - х ).