> f3:= x -> x^2 / (2 * x + 5);

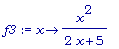
> plot(f3(x), x = -5..5,y = -25..25, color = red);

Упростим дробь:

f3 = 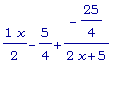. Теперь очевидно, что

y = 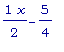- наклонная асимптота.

> D(f3);

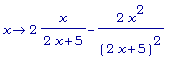
> simplify( 2*x/(2 * x + 5) - 2 * x^2 / (2*x + 5)^2);

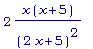
Следовательно, критической является точка x = 0, -5.

Отметим, что 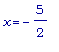не будет являться критической точкой, т.к. и функция здесь не определена.

Чтобы выяснить, где f3 '(x) положительна, а где - отрицательна, достаточно исследовать на знак произведение ,

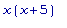т.к. множитель 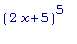неотрицателен.

> plot(x*(x+5), x = -10..10, color = red);

Значит, f3возрастает на ( - 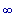,-5) и (0, ).

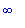Функция f3 убывает на ( 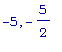) и ( 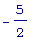,0). Напомним, что функция НЕ дифференцируема в точке x = .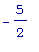

Следовательно, f3 имеет локальный максимум в точке x = -5 и локальный минимум - в точке x = 0.

Обратимся к выпуклости.

> D(D(f3));

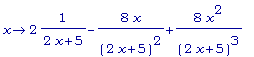
> simplify( 2*1/(2*x+5)-8*x/((2*x+5)^2)+8*x^2/((2*x+5)^3) );

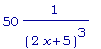
Итак, f3 ''(x) = .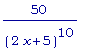

ВЫВОДЫ: график f3 направлен выпуклостью вниз на ( 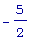, 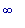), а выпуклостью вверх - на (- , ).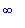

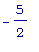Направление выпуклости меняется при переходе через точку х = 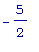, но т.к. x = 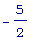не принадлежит области определения функции, то точек перегиба нет.

> a3:= plot(f3(x), x = -10..10, y = -25..25,color = red):

> b3:= plot(1/2 * x - 5/4, x = -10..10, color = magenta):

> display({a3,b3});