> f2:= x -> surd(x,3)^5 - 5 * surd(x,3)^2;

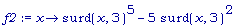
> plot(f2(x), x = -10..10, color = red);

> D(f2);

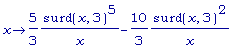
Слишком туманно! Лучше мы найдём производную старым проверенным способом, т.е. вручную:

f2 '(x) =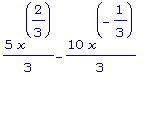

= .

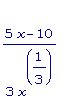Итак, f2 '(x) = 0 когда x = 2, и, кроме того, f2 '(x) , в отличие от функции, не определена в точке x = 0.

Следовательно, имеются две критические точки: x = 0 и х = 2. Постройте график f2 '(x). Т.к. f2 '(x) не определена

в нуле, постройте график сначала для отрицательных значений x , а затем - для положительных.

ВЫВОДЫ: f2 возрастает на (- 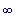,0) и (2, ).

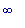f2 убывает на (0,2).

Следовательно, f2 обладает локальным максимумом в точке x = 0 и локальным минимумом в точке x = 2.

Функция НЕ дифференцируема в точке x = 0.

Теперь обратимся к направлению выпуклости.

> D(D(f2));

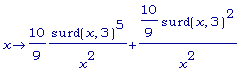
Опять, слишком громоздко! Лучше мы сделаем сами:

f2 ''(x) = = .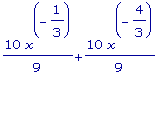

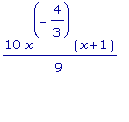Очевидно, что f2 ''(x) = 0, когда x = -1. Кроме того, производная не определена в точке x = 0.

Постройте график f2 ''(x). И вновь рекомендуем "склеить" его из двух частей: до точки x = 0 и после.

ВЫВОДЫ: график функции f2 направлены выпуклостью вниз на (-1,0) и (0, ) ,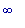

и вверх - на промежутке (- 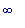,-1).

Имеется одна точка перегиба: x = -1.

Асимптот нет.