> g4:= x -> surd(x-4,3) * 2 * x;

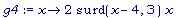
> plot(g4(x), x = -5..7);

Судя по графику, у функции должен быть один миниму и ни одного максимума.

> D(g4);

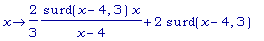
> simplify( (2/3) * (surd(x-4,3)*x)/(x-4) + 2 * surd(x-4,3));

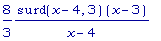
Из последней формулы следует, что у функции имеется две критические точки: x = 4 and x = 3. В первой из них функция существует, а производная - нет. Во второй точке производная обращается в ноль.

Дальнейшее упрощение даёт

g4' (x) =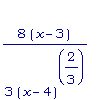

Т.к. знаменатель всегда неотрицателен (там, где определён), мы заключаем, что

g4'(x) > 0 если x > 3. Следовательно, g4 возрастает, если x > 3.

Кроме того, g4 имеет локальный минимум в точке x = 3.

Теперь мы должны разобраться с выпуклостью.

> D(D(g4));

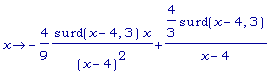
> simplify( -4/9*surd(x-4,3)*x/((x-4)^2)+4/3*surd(x-4,3)/(x-4));

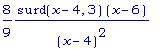
Значит, g4''(x) = 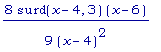. Легко заметить, что

g4''(x) > 0 , если x < 4 или x > 6.

Откуда, можно сделать выводы: график g4 направлен выпуклосьтю вниз, если х принадлежит (- 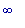, 4) и (6, 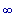) , и направлен выпуклостью вверх, когда х принадлежитan (4,6). Следовательно, график имеет две точки перегиба: x = 4, х = 6.

Получше приглядимся к изменению направления выпуклости графика функции в точке x = 6.

> plot(g4(x), x = 4..7, color = black);

> shape_plot(g4,4,7);