Вначале отметим, что функция в точке x = 0 не определена.

Предел g(x) при стремлении х к плюс (или минус) бесконечности, равен 1, а значит, у графика функции имеется горизонтальная асимптота

y = 1.

> g3:= x -> (3 + x^2) / ( x^2);

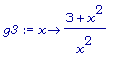
Построим график этой функции, что позволит оценить её поведение.

> plot(g3(x), x = 1..4, color = black);

> plot(g3(x), x = -4..-1, color = black);

Из графика следует, что у функции нет экстремумов, что она возрастает там, где x <0 , и убывает там, где x > 0. График же направлен выпуклостью вниз как на промежутке ( - , 0) , так и на промежутке (0, ).

Точек перегиба нет. .

> D(g3);

> simplify( 2 /x - 2*(3 + x^2)/(x^3));

Итак, g3' (x) = 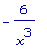, а потому критических точек нет.

Далее, g3''(x) = , т.е. вторая производная положительна всюду (кроме х=0).

Следовательно, наша догадка правильна.

> shape_plot(g3,-4,-1);