> g2:= x -> x * sin(x);

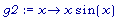
> plot(x * sin(x), x =-1..7);

График позволяет утверждать, что у функции имеется один локальный максимум и два локальных минимума.

> D(g2);

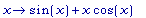
Интересуемся точками, в которых g2' (x) = 0 (во всех точках промежутка функция и её производные определены).

Когда x = 0, мы имеем g2'(x) = 0 и, следовательно, 0 - одна из критических точек.

Приравняв g2' (x) = 0, и разделив обе части этого уравнения на cos(x), мы получим: tan(x) = -x.

Построим графики функций y = tan(x) и y = -x и найдём точки пересечения этих графиков. Сделаем три графика, минуя точки, в которых тангенс не определён.

> a2:= plot(tan(x), x = 0..Pi/2 - .1, color = black):

> b2:= plot(-x, x = 0..4, color = blue):

> bb2:= textplot([3,5,`PLOT 1`], color = magenta):

> display({a2,b2,bb2});

> c2:= plot(tan(x), x = Pi/2 + .1..(1.5)*Pi - .1, color = black):

> d2:= plot(-x, x = 0..5, color = blue):

> dd2:= textplot([2,5,`PLOT 2`], color = magenta):

> display({c2,d2,dd2});

> e2:= plot(tan(x), x = (1.5)*Pi + .1.. 2* Pi, color = black):

> f2:= plot(-x, x = 0..7, color = blue):

> ff2:= textplot([2,-6,`PLOT 3`], color = magenta):

> display({e2,f2,ff2});

Из первого графика следует, что х = 0 - критическая точка. А из второго и третьего графика следует, что ещё имеется ровно одна критическая точка, принадлежащая промежутку ( /2, 3 /2), назовём её c1, и одна критическая точка на промежутке(3 /2, 2 ), назовём её c2.  Найдём численные значения c1 и c2.

> fsolve(tan(x) = -x, x = Pi/2.. 3*Pi/2);

> fsolve(tan(x) = -x, x = 3*Pi/2.. 2*Pi);

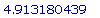
Итак, имеем три критические точки: x = 0, x = c1 ~ , and x = c2 ~ .

Отметим, что g2' (x) > 0 если sin(x) > -x cos(x) . В предположении, что cos(x) > 0, это неравенство сводится к

tan(x) > -x для x из [0, /2) или x из (3 /2, 2 ].

Если же cos(x) > 0, то неравенство сводится к виду tan(x) < -x для x из ( /2, 3 /2).

Из графиков 1,2,3 мы видим, что g2' (x) > 0 если x принадлежит (0, /2), (c2, 2 ) или ( /2,c1).

Следовательно, g2 возрастает, если x принадлежит промежуткам (0, /2), (c2, 2 ), ( /2,c1).

Значит, g2 имеет локальный min, когда x = 0, c2 , и локальный max , когда x = c1.

Теперь обратимся к направлению выпуклости графика.

> D(D(g2));

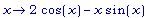
Отсюда: g2'' (x) > 0 , если 2 cos(x) > x sin(x) . А это нервенство сводится для sin(x) > 0 к виду 2 cot(x) > x для x из (0, ),

или к виду 2 cot(x) < x для x из ( ,2 ), т.е. когда sin(x) < 0 .

Вновь, мы построим y = cot(x) и y = x.

> h2:= plot(cot(x), x = 0.1..Pi-.1, color = black):

> i2:= plot(x/2, x = 0..4, color = blue):

> j2:= textplot([1,6,`PLOT 1`], color = magenta):

> display({h2,i2,j2});

> k2:= plot(cot(x), x = Pi + .1 .. 2*Pi - .1, color = black):

> l2:= plot(x/2, x = 3..7, color = blue):

> m2:= textplot([4,8,`PLOT 2`], color = magenta):

> display({k2,l2,m2});

Пусть e1 - единственная точка из промежутка ( 0, ) , где 2 cot(x) = x

и пусть e2 - единственная точка из промежутка ( , 2 ) , где 2 cot(x) = x. Тогда, g2''(x) > 0 если x принадлежит (0, e1) или (e2, 2 ).

Значит, график функции g2 направлен выпуклостью вниз, когда x находится в (0, e1) или (e2, 2 ).

Обе точки: и x = e1, и х = e2 - точки перегиба.

Получим численные значения e1,e2.

> fsolve(D(D(g2))(x) = 0, x, 0.1.. Pi - .1);

> fsolve(D(D(g2))(x) = 0, x, Pi + .1.. 2 * Pi - .1);

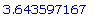
Откуда, e1 ~ и e2 ~ .

> shape_plot(g2,-1,7);