Пусть .

a) Найти линейную аппроксимацию для f(x) , когда x = 1.

b) Построить график f(x) и её аппроксимацию в одних осях.

c) Используя линейную аппроксимацию, вычислитьse the linear approximation to estimate, .

Сравнить полученное значение с фактическим.

d) Вычислить y и dy, для x = 1 и x = 2.98.

Построить график f(x), линейную аппроксимацию и показать dy и y .

> f:= x -> sqrt(x + 3);

> D(f);

> df:= x -> (0.5) * ( 1 / (sqrt(x + 3)));

> f(1);

> df(1);

Таким образом, линейная аппроксимация (т.е. касательная), проходит через точку (1,2)

и имеет угловой коэффициент .25 .

> L:= x -> 2 + 0.25 * ( x - 1);

a) Следовательно, линейная аппроксимация есть: L(x) = 1.75 + 0.25 x .

> plot({f(x),L(x)}, x = -5..5, color=[brown,blue]);

Из графика достаточно очевидно: линейная аппроксимация f (x) НЕ хороша всюду, за исключением окрестности точки 1.

> plot({f(x),L(x)}, x = 0.5..1.5, color=[brown,blue]);

Для значений x , близких к 1, линейную аппроксимацию можно считать удовлетворительной.

> L(3.98);

> f(3.98);

c) Линейное приближение функции даёт значение 2.7450 для корня квадратного ,

в то время как вычисления с точностью до десятого знака дают

d) Обратимся к части (d) задачи.

> f(3.98) - f(1);

Следовательно, y = (для x = 1 и x = 2.98).

> df(1) * 2.98;

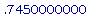
Значит, dy = (для x = 1 и x= 2.98).

> L(3.98);

> f(1);

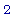
> L(1);

> f(3.98);

> with(plots):

> A:= plot({f(x),L(x)}, x = 0..6, color=[blue,brown]):

> B:= plot([t,2, t = 1..3.98], color = magenta):

> C:= plot([3.98,t,t = 2..2.7450], color = magenta):

> F:= plot([t,2.641968963, t = 3.98..4.2],color = black):

> G:= plot([4.2,t,t = 2.641968963..2.7450], color = black):

> H:= plot([t,2.7450, t = 3.98..4.2],color = black):

> K:= textplot([4.5,2.7,'dy'], align=RIGHT, color = red):

> L:= textplot([4.2,2.3,'deltay'], align=RIGHT, color = red):

> M:= textplot([2.3,1.9,'deltax'], color = red):

> display( {A,B,C,F,G,H,K,L,M}, axes = boxed);