Математический анализ в Maple

Поставим перед собой первую задачу: имея неявную функцию, можно ли построить её график так, чтобы были видны все её индивидуальные особенности?

Начнём с 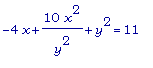, и найдём все точки с абсциссой х = 2.

> restart; with(plots):

> imp_fun := -4*x + 10*(x^2) * (y^(-2)) + y^2 = 11;

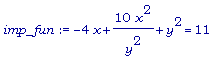
Наш метод будет содержать два шага : во-первых, в подстановке значения x, и, во-вторых, в решении получившегося уравнения относительно y.

Подставим x= 2 в неявное уравнение.
Получим уравнение, содержащее всего одну переменную..
Получим точное решение уравнения в радикалах. Мы также можем конвертировать точное решение в приближенную десятичную форму.

> subs( x = 2, imp_fun );

> s := solve( % );

> s := evalf( % );

Построение графиков неявных функций открывает перед нами совершенно новый мир дизайна. А ведь раньше это представлялось довольно сложной задачей, отнимающей чрезмерно много времени, и с которой без дополнительных технологических средств эффективно никто не справлялся. Результаты можно получить просто фантастические. Мы бы их сравнили с ароматным листовым чаем, заваренным из из многих самих по себе замечательных сортов. Такого настоя вряд ли можно добиться от явных, а потому и графически "прозрачных" функций.

Теперь нам понадобится не простейшая графическая команда plot , а специальная - implicitplot.

Первая особенность, которую мы должны отметить в поведении неявных функций: графики многих из них не проходят тест вертикальными линиями! (Т.е. некоторые вертикали имеют более одной общей точки с графиком неявной функции). Вот Вам и первая причина особого интереса к неявным функциям.

Возьмём, например, наклонный эллипс.

Неявной уравнение , область х, область у.

> implicitplot( x^2 + x*y + y^2 = 16, x = -5..5, y = -5..5, grid=[50,50] );

[Maple Plot]

Некоторые из форм замечательно просты.

> implicitplot( x^4 + 8*(x^3) + y^4 = 16, x = -12..10, y = -10..10, grid=[50,50],thickness = 2, color = brown, scaling = constrained);

[Maple Plot]

С другой стороны, некоторые функции с графической точки зрения - столь же замечательно сложны. Иногда следует как можно больше увеличить число точек рисунка, используемых для построения, чтобы разобраться в хитросплетениях линий. Первое же впечатление, полученное от графика с опциями по умолчанию, может быть очень и очень обманчивым. Простое увеличение точек графика опцией grid подчас даёт совершенно иное "полотно".

> implicitplot( x*y*cos(x^2 + y^2) = 1, x = -10..10, y = -10..10, grid=[30,30] );

[Maple Plot]

> implicitplot( x*y*cos(x^2 + y^2) = 1, x = -10..10, y = -10..10, grid=[80,80] );

[Maple Plot]

Многие из этих графиков обладают различными видами симметрии.

Вот, например, симметрия относительно оси у .

> implicitplot( x^2 + 1.5*y*x^2 + y^2 = 1, x = -10..10, y = -10..10, grid=[50,50] );

[Maple Plot]

> implicitplot( (x^2 + y^2 -2) = (.5 + y*x^2)^2 , x = -5..5, y = -5..5, grid=[100,100] );

[Maple Plot]

Теперь представим график, симметричный относительно оси х .

> implicitplot( -4*x + 10*(x^2) + (y^(-2)) + y^2 = 11, x = -5..5, y = -5..5, grid=[100,100] );

[Maple Plot]

А вот график с двумя взаимно перпендикулярными осями симметрии - осями х и у:

> implicitplot( x^2 - y^2 = x*y*sin(x*y), x = -4..4, y = -3..3, grid=[100,100] );

[Maple Plot]

А вот график, симметричный относительно прямой y = -x:

> implicitplot( x - y + sin(2.5*x*y) = sin(x) - sin(y) + sin(x*y), x = -5..5, y = -5..5, grid=[100,100] );

[Maple Plot]

Некоторые из графиков обладают таким видом симметрии, который не так-то просто и описать:

> implicitplot( (x*y)*sin(y) = x*cos(x-y), x = -10..10, y = -10..10, grid=[100,100]);

[Maple Plot]

Вот ещё один пример графика со сложными деталями: здесь тоже имеется намёк на какой-то вид симметрии. Но элементарных знаний для её описания уже не хватает.

> implicitplot( ln( (x + 7*sin(y))^2 ) = exp(y + 2*cos(x)) , x = -9..9, y = -12..3, grid=[100,100]);

[Maple Plot]

А этот график напоминает сложенную из паззлов картинку на плоскости (вид сзади):

> implicitplot( sin(x + 2*sin(y) ) = cos( y + 3*cos(x)), x = -10..10, y = -10..10, grid=[100,100]);

[Maple Plot]