При построении графиков неявных функций мы использовали команду implicitplotвместо стандартной и привычной команды plot . Точно так же и при дифференцировании этого вида функций следует использовать команду implicitdiff вместо хорошо уже Вам знакомой diff .

> implicitdiff( -4*x + 10*(x^2)*(y^(-2) ) + y^2 = 11, y, x);

В состав команды кроме уравнения, определяющего неявную функцию, входит указание зависимой и независимой переменных (у и х в нашем случае). Обратите внимание: результат дифференцирования - функция двух переменных (х и у ).

Т.к. неявная функция часто имеет несколько значений для одного и того же значения аргумента х , можно наблюдать и большое количество касательных к графику неявной функции в точках с одинаковой абсциссой.

В следующем примере мы рассмотрим несколько шагов, необходимых для построения всех касательных к графику функции в точках с абсциссой x = 2.

Начнём с уже знакомой функции:

> imp_fun := -4*x + 10*(x^2)*(y^(-2)) + y^2 =11;

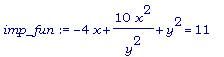
Шаг 1 : Выберем значение х (c):

> c := 2;

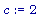
Шаг 2 : Вычислим соответствующие значения y:

> s := evalf( solve( subs( x = c, imp_fun)));

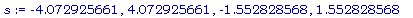
Шаг 3 : Вычислим значения углового коэффициента касательных, проведенных к графику функции в соответствующих точках. Вы не за были, что производная в нашем случае - неявная функций как х , так и у? Т.к. имеем четыре разных значения у, то и значений углового коэффициента будет 4. x = c, имеем четыре различных значения у и 4 различных угловых коэффициента.

> m1 := evalf( subs ( { x = c, y = s[1] }, implicitdiff( imp_fun, y,x)));

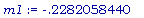
> m2 := evalf( subs ( { x = c, y = s[2] }, implicitdiff( imp_fun, y,x)));

> m3 := evalf( subs ( { x = c, y = s[3] }, implicitdiff( imp_fun, y,x)));

> m4 := evalf( subs ( { x = c, y = s[4] }, implicitdiff( imp_fun, y,x)));

Находим значение углов наклона для каждого из 4 значений, выполняя подстановку x = c в неявной производной для каждого из случаев.

Шаг 4 : Потроим гарфик функции и 4 касательные:

> implicitplot( {y - s[1] = m1*(x-c), y - s[2] = m2*(x-c), y - s[3] = m3*(x-c), y - s[4] = m4*(x-c), imp_fun }, x = -5..5, y = -5..5, grid=[100,100]);