> c := cone([0,0,4], sqrt(8), -4, color=green):
t := pointplot3d([[0,0,0], [sqrt(8),0,0], [0,0,4],[0,0,0]], connect=true, color=black, thickness=2):
ground := plot3d(0,x=-3..3,y=-3..3,color=grey,grid=[5,10], style=patchnogrid):
display([c,t,ground],scaling=constrained, style=wireframe, orientation=[40,60]);

Пусть а - катет-основание прямоугольного треугольника, а b - его катет-высота. Известно, что гипотенуза равна 3. Объём получившегося конуса может быть вычислен тогда по формуле: . Нам следует максимизировать объём.

Т.к. имеем дело с прямоугольным треугольником, то  .

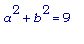> restart:

> evalf(Pi);

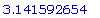
> V:= (1/3) * (3.141592654) * (9 - b^2) * b;

> plot(V(b), b = 0..3);

Из графика следует, что наши попытки не бесперспективны. Точку максимума будем искать как корень уравнения 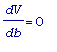. Решим это уравнение :

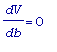> VV:= b -> (1/3) * Pi * (9 - b^2) * b;

> diff(VV(b),b);

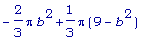
> solve(%=0,b);

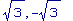
> evalf(sqrt(3));

Конус обладает наибольшим объёмом в том случае, когда b = sqrt(3) и

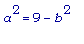= 9 - 3 = 6, т.е.,

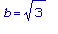и .
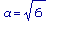