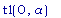Посмотрим вначале на графическое толкование ситуации.
>
f := x->exp(-x);
a1 := 1.5: a2 := 2.5:
eqTanLine := (x,a) -> f(a) + (x-a) * D(f)(a):
b1 := solve( eqTanLine(x,a1)=0, x):
b2 := solve( eqTanLine(x,a2)=0, x):
graph := plot( f(x), x = 0..5, thickness=2):
tanLine1 := plot( eqTanLine(x,a1), x = 0..b1, color=blue, thickness=2):
tanLine2 := plot( eqTanLine(x,a2), x = 0..b2, color=green, thickness=2):
line1 := line( [0, 0],[b1, 0], color=blue, thickness=2):
line2 := line( [0, 0],[0, eqTanLine(0,a1)], color=blue, thickness=2):
line3 := line( [0, 0],[b2,0], color=green, thickness=2):
line4 := line( [0, 0],[0, eqTanLine(0,a2)], color=green, thickness=2):
display( graph, tanLine1, tanLine2, line1, line2,line3, line4);
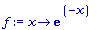
![[Maple Plot]](xxx.files/C1-1031.gif)
Из приведенного графика следует, что вид треугольника существенно зависит от того, как проведена касательная.
Мы должны найти такое положение касательной, при котором площадь образовавшегося треугольника будет наибольшей.
Найдём абсциссу точки пересечения касательной и оси х.
>
solve( exp(-a)-exp(-a)*(x-a)=0,x);
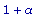
Таким образом, если x = a , то абсцисса точки пересечения касательной и оси х есть 1 + a.
Найдём ординату точки пересечения касательной с осью у .
>
tl(0,a);