Производитель тонких оловянных канистр изготовляет канистры объёмом в 80 кубических дюймов.

a) Укажите наименьшее количество олова, необходимое на изготовление такой канистры.

Для начала, ответим на первый вопрос, (a) . Пусть r - радиус основания канистры, а

h - её высота. Воспользуемся общеизвестными формулами для объёма и площади поверхности канистры-цилиндра:

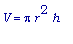= 80 , .

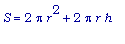Из первого уравнения следует, что 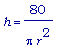, и мы получаем:

.

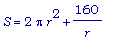Мы желаем минимизировать S.

> g3:= r -> 2 * Pi * r^2 + 160/r;

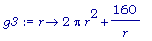
> plot(g3(r), r = 1..5);

Как следует из графика функции g3, имеется единственное минимальное значение. Уточним его значение.

> fsolve(D(g3)(r) = 0, r = 0..4);

> D(D(g3))(2.335088650);

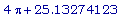
> g3(2.335088650);

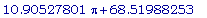
Следовательно, функция g3 обладает критическим значением в точке r = ;  вторая производная g3 в этой критической точке положительна, а это свидетельствует о том, что g3 имеет здесь минимум.

ВЫВОД: Минимальный расход олова будет при площади поверхности канистры, равной :

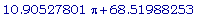
Теперь решим вторую часть задачи, (b).

> h3:= r -> (80)/(Pi * r^2);

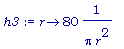
> h3(2.335088650);

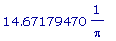
Вывод: При минимальной площади поверхности канистры с данным фиксированным объёмом SA, радиус канистры равен 2.335088650, а её высота - .