Найти минимальное расстояние от точки кривой до точки (1,-1).

Существует ли максимальное расстояние? Если да, то найдите его.

Предалагаем графическую иллюстрацию решения.

> with(plots):

> f2:= x -> x^2 + 1;

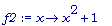
> a2:= plot(f2(x), x = -2..3, color = black):

> b2:= line([1,-1], [0, f2(0)], color=red, linestyle=1):

> c2:= line([1,-1], [2, f2(2)], color=red, linestyle=1):

> d2:= line([1,-1], [-1, f2(-1)], color=red, linestyle=1):

> display([a2,b2,c2,d2]);

Из предложенного графика мы видим, что на графике функции y =

невозможно выбрать точку так, чтобы расстояние от ней до точки (1,-1) было бы максимальным. Зато очевидна перспективность поисков точки, минимально удалённой от данной.

Квадрат этого расстояния: g2:= .

Минимизируем g2.

> g2:= x -> (x - 1)^2 + ( x^2 + 2)^2;

Посмотрим на график g2 , помня о том, что мы интересуемся минимумом.

> plot(g2(x), x = 0..5);

> plot(g2(x), x = 0..1);

> fsolve(D(g2)(x) = 0, x = 0..4);

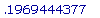
Мы нашли критическую точку:

> evalf(D(D(g2))(.1969444377));

Т.к. вторая производная в этой точке >0 , g2 достигает в критической точке минимума.

ВЫВОД: Когда x = 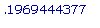, расстояние от точки ( )

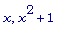до точки (1,-1) минимально.