У треугольника одна сторона имеет длину 5 , а вторая - 8.

a) Каким должен быть угол между сторонами, чтобы площадь треугольника была наибольшей?

b) Каким должен быть периметр треугольника, чтобы его площадь была наибольшей?

Решим вначале первую задачу, (a) . Обозначим площадь треугольника как A , а угол между двумя данными сторонами длин 5 и 8 - как b .

Тогда

A = (1/2) * 5 * 8 * sin(b) =

Мы хотим максимизировать A.

> A4:= b -> 20 * sin(b);

> plot(A4(b), b = 0..2*Pi, color = black);

Из графика следует, что на промежутке от 0 до 2Pi у функции всего лишь один максимум.

> fsolve(D(A4)(b) = 0, b = 0..Pi);

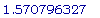
> D(D(A4))(1.570796327);

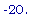
Критическое значение площади A на промежутке от 0 до Pi есть:

К тому же, A''( ) < 0.

ВЫВОД: площадь треугольника максимальна, когда угол между данными сторонами равен радиан.

Решим часть (b) задачи.

Обозначим длину третье стороны треугольника как c .

Напомним, что угол между сторонами длиною в 5 и 8 бы обозначили как b.

Из теоремы косинусов следует:

= .

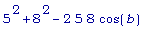> c:= sqrt(25 + 64 - 80 * cos(1.570796327));

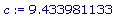
> P:= 9.433981133 + 5 + 8;

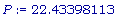
Периметр треугольника наибольшей площади равен .