> restart;

Теперь обратимся к нашей другой проблеме: как определить мгновенную скорость движущегося объекта? Для определённости, предположим, что объект перемещается вдоль 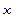-оси так, что его положение в любой момент времени задается выражением . Например, Мы можем положить 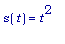, или 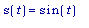. ( Как перемещается объект в обоих этих случаях?)

Наше исследование можно начать с того, что не составит особого труда: с определения средней скорости движения. Используя элементарную формулу "Расстояние =Скорость, умноженная на Время". Пусть объект был в пути временной интервал . Если разделить расстояние между начальной и конечной точкой движения, на временной интервал, то мы и получим значение средней скорости движения объекта.

Средняя скорость в течении временного интервала = .

Вот простейшая процедура для вычисления (в десятичном приближении) средней скорости:

> av := proc(s,t0,t1) evalf((s(t1) - s(t0))/(t1 - t0)) end proc:

Мы можем теперь определить функцию движения и вычислять средние скорости.

> s := t-> t^2 ;

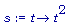
> av(s,1,5);

(Желательно, чтобы Вы проверили результат вручную.) Конечно, наша задача состоит отнюдь не в вычислении средней скорости за интервал , а в вычислении мгновенной скорости в некоторый момент времени . Решение состоит в том, чтобы продолжать вычислять средние скорости, но с каждым разом за все более короткий временной интервал вблизи точки . Вот несколь результатов для нашей последней функции движения:

> av(s,1,2); av(s,1,1.5); av(s,1,1.1); av(s,1,1.01);

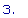
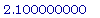
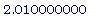
Экспериментируя с достаточным количеством временных интервалов, можно прийти к выводу, что чем ближе по времени к моменту мы будем вычислять значение средней скорости, то тем ближе это значение будет к 2. Конечно, мы не можем положить :

> av(s,1,1);

Error, (in av) division by zero

Однако, изменение значения средней скорости происходит гладко при стремлении к . Мы говорим, что средняя скорость имеет предел при стремлении к , и есть все основания полагать, что этим пределом и будет мгновенная скорость объекта в точке :

Мгновенная скорость в момент времени = .

Теперь, в частности, видно, что точно к такому же пределу мы пришли и при решении задачи о касательной. Это станет ещё более очевидным, если мы введём новую переменную такую, что , и , в результате чего предел несколько видоизменится:

Мгновенная скорость в момент = .

Получается так, что мгновенную скорость можно интерпретировать как угловой коэффициент касательной, проведенной к графику некоторой функции. Фактически, сравнивая решения двух наших задач, можно утверждать, что мгновенная скорость численно равна угловому коэффициенту касательной, проведенной к графику функции движения s.

Предлагаем рисунок для функции движения 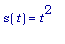, что мы использовали ранее. Вы можете видеть, что касательная линия, проведенная к графику функции в точке (1;1) имеет угловой коэффициент 2, как мы были вправе ожидать и в результате расчетов по средней скорости.

> s := t-> t^2 ;

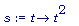
> plot([s(t),s(1)+2*(t-1)], t=-1..3, colour=[black,red]);