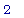Подведём итоги: мы видели два применения предела . Его геометрической интерпретацией является угловой коэффициент касательной, проведенной к графику функции в точке ( , ). Если же под функцией понимать закон движения объекта, то этот предел представляет мгновенную скорость объекта в момент времени . Оба эти примера приводят к одной и той же идее: указанный предел представляет мгновенную скорость изменения функции  . Всему полезному стоит давать свои мена. Наш предел называется производной функции (в точке ), и обозначается ' ( ) . ( Maple использует символ D(f) вместо ' .) Т.к. значение предела зависит от выбора точки , то он является функцией, и мы подчеркнём это, опустив индекс 0 у х, а производной приписав аргумент:

' ( ) = .

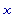Например, приведём значения некоторых производных, найденных при помощи Maple . Понаблюдайте, какие при взятии производных получаются функции, какие значения принимают производные в выбранных точках. (Они Вам ничего не напоминают? В смысле изложенного выше материала?)

> f := x-> 3*(1-x)*x^2 ;

> f1 := D(f);

> D(f)(.1);

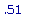
> D(f)(1);

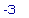
> D(f)(0);

> g := x-> x^2 ;

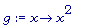
> D(g)(1);