Введём обозначения h, x, и y так, как это показано на рисунке.
>
restart;
>
A1:=plots[textplot]({[2.6,1.9,'L'],[3.7,2,'h'], [.1,1.1,`y`],[.5,.3,`x`],},align=RIGHT):
>
A3:=plot({[[0,0],[0,8],[4,8],[4,4.45],[1.219,0], [0,0]],[[4,4.45],[0, 2.5],[1.219,0]]},color=blue):
>
A4:=plot([[4,4.45],[4,0],[1.219,0]],color=red):
>
A5:=plots[polygonplot]([[4,4.45],[0,4.45],[0,2.5]], style=patch,color=tan):
>
plots[display]([A1,A3,A4,A5],axes=boxed, scaling=constrained);
![[Maple Plot]](xxx.files/C1-101.gif)
Из рисунка легко вывести несколько уравнений, связывающих x, y, h, и L . Например, по теореме Пифагора из маленького (по рисунку) прямоугольного треугольника с катетами х и у следует уравнение eq1:
>
eq1 := y^2+x^2=(4-x)^2;
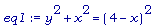
eq2 выведем по той же теореме из правого прямоугольного треугольника с искомой гипотенузой L и катетами длин h и 4-x:
>
eq2 := L^2 = (4-x)^2 + h^2;
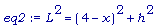
Легко заметить, что коричневый треугольник с гипотенузой h и катетами 4 и h-y подобен левому "маленькому" треугольнику с гипотенузой 4-x и катетами y и x. Это позволит нам составить уравнение eq3:
>
eq3 := 4/(h-y)=y/x;
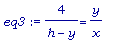
>
h := solve(eq3,h);
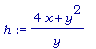
>
x := solve(eq1,x);
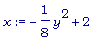
>
L := unapply(sqrt(op(2,simplify(eq2))),y);

В результате мы получили выражение для L как функцию переменной y. Имея под рукой Maple, легко оценить поведение этой функции, построив её график:
>
plot(L,2..4);
![[Maple Plot]](xxx.files/C1-108.gif)
Мы видим, что минимальное значение длины перегиба примерно равно
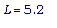 дюйма и достигается оно, когда
дюйма и достигается оно, когда
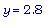 дюйма. Мы можем получить более точное значение, используя функцию
fsolve
дюйма. Мы можем получить более точное значение, используя функцию
fsolve