Интегрируемые Функции
Хотя функции должны быть непрерывными и гладкими, чтобы, в свою очередь, быть дифференцируемыми, площадь может быть найдена без особых сложностей и для фигур, ограниченных линиями, не являющимися ни гладкими, ни непрерывными. Такие функции мы будем называть интегрируемыми по причинам, которые будут ясны в ближайшем будущем.
Можно говорить о площади даже фигур, ограниченных графиками крайне "подозрительных функций": разрывных, сшитых из кусков или даже всюду не дифференцируемых!
>
f:= x -> piecewise( x < 2, -1, x<6, 2-x/2, x < 8, .5*x^2 - 6*x + 18, 1);
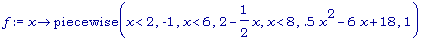
>
a:=0; b := 10; area_plot( f(x), a, b );
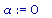
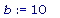
![[Maple Plot]](xxx.files/C1-23R15.gif)
>
f := x-> sqrt( abs(x^2 - 9 )) - 2;
a := -5; b := 5; area_plot( f(x), a, b );
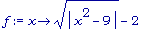
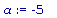
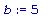
![[Maple Plot]](xxx.files/C1-23R19.gif)