Пусть y(t) -
температура
несчастной птицы
через t минут.
Согласно Закону
Охлаждения
Ньютона, имеем:
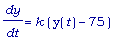 .
.
Тогда
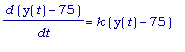 , откуда
, откуда
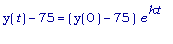 .
.
Следовательно,
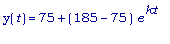
Мы получили, что
y(30) = 150 =  => l
=> l  .
.
Итак,
температура
индюшки через t
минут есть:
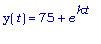 , где
, где
 .
.
>
evalf(ln(75/110)/30);
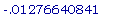
(a)
Нас интересует
y(45).
>
y:= t -> 75 +
110 *
exp(-.01276640841
* t);
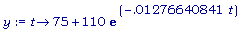
>
y(45);

Таким образом,
через 45 минут
температура
индюшки
опустится до  F .
F .
(b) Мы хотим
установить
момент времени,
когда y(t) =
100.
>
fsolve( 75 + 110
*
exp(-.01276640841
* t) = 100, t);

Численно мы
определили, что
потребуется 1
час и 56 минут
для того, чтобы
индюшка остыла
до температуры
100F.
Можем решить
задачу и без
помощи Maple:
 =>
=>
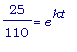 =>
=>
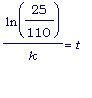 .
.
Следовательно,
необходимо
 минут для того,
чтобы
температура
индюшки упала до
100 F, причём
минут для того,
чтобы
температура
индюшки упала до
100 F, причём
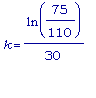 .
.
>
evalf(
ln(25/110) / (
ln(75/110) /
30));
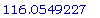
Отметим, что
наши ответы
находятся в
хорошем
согласии.
>
plot(y(t),t =
0..120, color =
red);
![[Maple Plot]](xxx.files/C1-20R69.gif)