В каком месте отрезка АВ следует выбрать точку P, чтобы угол был максимальным? (См. рисунок). Чему равно максимальное значение ?

> X := 1:
ground := line([0,0],[3,0], color=brown, thickness=3):
stake1 := line([0,0],[0,5], color=blue, thickness=2):
stake2 := line([3,0],[3,2], color=blue, thickness=2):
line1 := line([X,0],[0,5], color=red, linestyle=2, thickness=2):
line2 := line([X,0],[3,2], color=red, linestyle=2, thickness=2):
text := textplot({[-.1,-.1,`A`],[X,-.1,`P`],[3,-.1,`B`], [X+.4,1.3,`theta`], [-.1,2.5,`5`],[3.1,1,`2`]}):
a := arc([1,0], 1, arccot((3-X)/2)..Pi-arccot(X/5)):
display(ground, stake1, stake2, line1, line2, text,a,axes=none,scaling=constrained);

Обозначим длину отезка AP как x .

Определим как функцию x.

Построим график этой функции и посмотрим, при каком значении максимально.

Что происходит с , когда x меняет своё значение от 0 до 3?

Имеем:

= - - .

Следовательно, = .

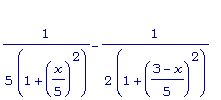Положив = 0 , получим уравнение:

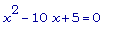Имеются две критические точки; однако следует учесть, что x расположен между 0 и 3 . Поэтому x = 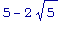- единственная устраивающая нас критическая точка.

> evalf( 5 - 2* sqrt(5));

> th:= x -> Pi - arccot(x/5) - arccot((3-x)/2);

> th(x);

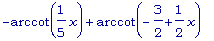
> plot(th(x), x = 0..3);

> evalf(th(0));

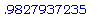
> evalf(th(.527864044));

Графическое поведение свидетельствует, что имеет максимум в точке

, который примерно равен 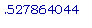единицам.

Мы можем использовать и тест первой производной, чтобы подтвердить, что в указанной критической точке функция имеет максимальное значение. Вы вполне можете справиться с этой задачей самостоятельно.

Из графика функции также следует, что при изменении аргумента x от 0 до 3, значения