Пусть некий объект при движении вдоль прямой подчиняется закону: .

Найти момент времени, в который мгновенная скорость равна средней скорости на отрезке [0, ].

Во-первых, построим график функции, задающей закон движения.

> s:= t -> t/2 - sin(t);

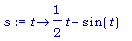
> plot(s(t), t = 0..Pi, color = red);

Из графика следует, что объект вначале движется в левом направлении, а затем - в правом.

Средняя скорость движения объекта на отрезке [0, ] даётся формулой:

( s( ) - s(0) ) / ( - 0 ) .

Мгновенная же скорость движения, как мы знаем, определяется производной s '(c). Итак, нас интересуют корни уравнения:

( s( ) - s(0) ) / ( - 0 ) = s '(c);

похоже, что нам удастся решить его точно.

> s(Pi);

> s(0);

> D(s);

Уравнение в явном виде: 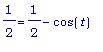для t из промежутка [0, ], или ещё проще: cos(t) = 0

для t из [0, ].

Корень: t = /2.

Построим график функции, на котором разместим и секущую, проведенную через точки

(0, 0) и ( , /2 ), а также касательную, проведенную к графику функции в точке t = /2 .

Эти прямые должны быть параллельны.

> D(s)(Pi/2);

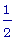
> s(Pi/2);

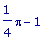
> with(plots):

> data:= ([0,0], [Pi, Pi/2]):

> a1:= plot( [data], color=magenta, thickness=2 ):

> a2:= plot(s(t), t = 0..5, color = green, thickness=2):

> a3:= plot((Pi/4 - 1) + 1/2 * ( x - Pi/2), x = 0..Pi, color = magenta, thickness=2):

> a4:= textplot([1/5,1,`Secant Line`], align={RIGHT}, color = blue, thickness=2):

> a5:= textplot([1.5,-.8, `Tangent Line`], color = blue):

> display({a1,a2,a3,a4,a5});