Получить квадратичное приближение для f (x) = вблизи a = 1.

Построить графики функций f (x) и P (x) в одних осях вблизи 1.

Построить графики функций f (x) и P (x) в одних осях, но уж для достаточно большой области изменения х ; является ли P(x) хорошим приближением для данной функции вдали от 1?

Определить значения x , для которых квадратичное приближение "грешит" не более чем на 0.01.

> f:= x -> 1/(1+x)^2;

> f(1);

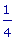
> D(f)(1);

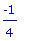
> D(D(f))(1);

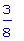
> P:= x -> 0.25 - 0.25 * (x - 1) + (3/16) * ( x - 1)^2;

> plot({f(x),P(x)}, x = 0..2, color=[blue,brown]);

> plot({f(x),P(x)}, x = 0..10, color=[blue,brown]);

Из приведенного выше графика следует, что P (x) НЕ являетмя хорошим приближением f (x) для x , далёких от 1.

Определим значения x , для которых | f(x) - P (x) | < 0.01, т.е.,

нас интересует случай, когда:

-0.01 < f (x) - P (x) < 0.01

или

f (x) - 0.01 < P (x) < f (x) + 0.01.

> g1:= x -> f(x) - 0.01;

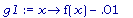
> g2:= x -> f(x) + 0.01;

> plot({P(x), g1(x), g2(x)}, x = 0.5..3, color=[blue, brown, magenta]);

> solve({-0.01 < f (x) - P (x), x > 0}, x );

> solve({f (x) - P (x) < 0.01, x > 0}, x);

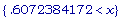
Из графического и аналитического решения следует, что условие | P (x) - f (x) | < 0.01 выполняется для