Настала пора на практике применить оператор D и функцию diff , чтобы вычилить некоторые производные. В процессе этого действа, мы будем иметь возможность проверить три основных правила дифференцирования. (Оставим на потом Цепное (Золотое) Правило , которое мы исследуем в другом worksheet.)

Во-первых, производная - линейна:

при любых константах и .

Во-вторых, верно правило для производной произведения:

.

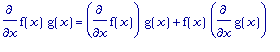В-третьих, верно правило для производной частного:

.

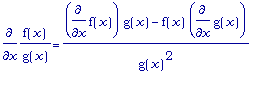Закон линейности - наиболее прост.

> diff(x^2, x); diff(x^3, x);

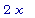
> diff(7*x^2 + 4*x^3, x); diff(5*x^2 - Pi*x^3, x);

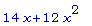
Выполним то же самое, но используя D .

> f := x -> cos(x^2); g := x -> x*exp(2*x);

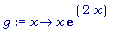
> D(f); D(g);

> D(3*f - g);

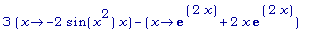
Если Вы внимательно всмотритесь в Maple-синтаксис , то заметите, что последний ответ подтверждает исследуемое правило, но слегка действует на нервы. А не попробовать ли, леди и сэры, паненки и господа, всё-таки вычислить значения производных в точке :

> D(3*f - g)(x);

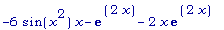
> 3*D(f)(x) - D(g)(x);

>

Теперь испытаем на прочность правила для производных произведения и частного, используя всё те же функции и .

Для начала, правило для произведения:

> D(f*g);

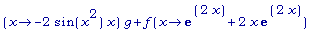
> D(f*g)(x);

> D(f)*g + f*D(g);

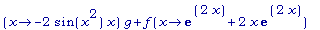
> D(f)(x)*g(x) + f(x)*D(g)(x);

В форме выражений, те же самые действия выглядят симпатичнее:

> diff(f(x)*g(x), x);

> diff(f(x), x)*g(x) + f(x)*diff(g(x), x);

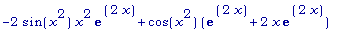
Нравится нам это или не нравится, но и в Канаде, и в Украине, и на Занзибаре при любых погодных условиях обе Maple-функции, хотя и в разных формах (что само по себе некоторым доставит эксклюзивное удовольствие, а некоторым - дополнительную зубную боль), свидетельствуют: правило для производной произведения работает!

Обратим наши взоры на правило дифференцирования частного:

> diff(f(x)/g(x), x);

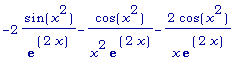
> simplify(%);

> (diff(f(x), x)*g(x) - f(x)*diff(g(x), x)) / (g(x))^2;

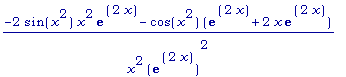
> simplify(%);

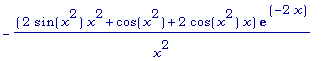
(Самое приятное и радостное предоставляем Вам, дорогие девчонки и мальчишки: проделайте тот же фокус, но используя оператор D .)