|
>
restart;
Довольно просто
написать
Maple
-процедуру,
которая
вычисляла бы
производную в
строгом
соответствии с
определением. (
Команда
unapply
применяется для
конвертации
выражения в
функцию.
)
>
myD := proc(f)
unapply(limit((f(x+h)-f(x))/h,h=0),
x) end:
>
f := x -> x^2;

>
myD(f);

>
myD(sin);
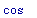
Может это и
смешно, но
встроенная в
Maple команда
D
делает то же
самое:
>
D(f);

>
D(sin);
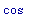
Отметьте, что
оператор
D
дифференцирует
функцию
,
и
что производная
- опять-таки
функция
(но, в общем
случае, совсем
иная, уже не от
Армани, а от
Версачи).
Например,
 можно вычислить
в точке:
можно вычислить
в точке:
>
D(f)(3);
D(f)(-5);
D(f)(0);



Важно, что
Maple
обладает и
другой командой
дифференцирования,
которая ближе по
духу к
классической
точке зрения на
производную
(речь идёт о
Maple-эквиваленте
обозначения
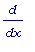 .) Команда
diff
дифференцирует
выражение,
и
выводит на
дисплей другое
выражение
.
.) Команда
diff
дифференцирует
выражение,
и
выводит на
дисплей другое
выражение
.
>
diff(x^2, x);
diff(x^3 + 5*x,
x);
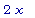
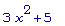
Заметьте, что
когда Вы
используете
diff,
то следует
указать
Maple
независимую
переменную
(аргумент
функции).
Попробуйте
предсказать
реакцию системы
на ввод
предлагаемой
ниже команды и
последующее
нажатие клавиши
<Enter>:
>
diff(x^2,y);

Вот и всё, чем
располагаем
Maple
для вычисления
производных
(если не
считать: 1)
наличия инертной
функции
Diff
,
предназначенной
для
конструирования
выражений в
почти
классическом
виде; 2)
различных
опций
в
упомянутых
командах.)
Не забывайте,
что производная
функции - тоже
функция (но
иная), что
производная
выражения - тоже
выражение (но
иное), и что они
вычисляются при
помощи
D
и
diff
соответственно.
Кроме всего
прочего, это -
милый пример
того, как
Maple
вынуждает Вас
ясно мыслить
.
Различие между
функциями и
выражениями не
было специально
надумано
Maple
-программистами:
это отражение
реального
положения вещей
в математике,
ответ на тот
факт, что для
производной не
зря используется
как обозначение
(') , так и
конструкция
 ,
что часто либо
не афишируется,
либо
игнорируется в
учебниках.
,
что часто либо
не афишируется,
либо
игнорируется в
учебниках.
|