> with(plots): with(plottools):
L1 := line([0,0],[18,0]):
L2 := line([0,9],[12,9]):
L3 := line([12,9],[12,15]):
L4 := line([18,0],[18,15]):
bar := rectangle([5,6], [15,7], color=blue):
display([L1,L2,L3,L4, bar], axes=none);

Мы решим эту задачу, отыскав минимум!

Пусть A и B обозначают концы трубы.

Длину трубы обозначим как L (длина отрезка от A до B ) и рассмотрим ситуацию, когда труба касается угла между прихожей и коридором.

Пусть (theta) - угол, образованный трубой и левой стенкой прихожей.

При стремлении к 0 или к /2, длина L стремится к .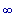

Найдём теперь угол, при котором L минимально. Труба такой длины "завернёт" за угол. Это и даст нам наибольшую из возможных длин трубы.

В уравнениях, прелагаемых ниже, положим x =

> L:= x -> 9 * csc(x) + 6 * sec(x);

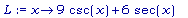
Вначале мы построим график функции L , чтобы составить впечатление о процессе.

Напомним, что функции csc(x) и sec(x) определены не при всех x. Из графика хорошо видно, что

может принимать значения от 0 до .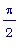

> plot(L(x), x = 0.1..Pi/2-0.1, color = black);

Вначале мы найдём минимум численно:

> fsolve(D(L)(x) = 0, x = 0..3);

> D(D(L))(.8527708776);

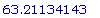
> L(.8527708776);

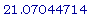
Т.е. численно мы получили критическую точку x = .

Т.к. вторая производная в критической точке положительна, то при x = у функции будет минимум. Численное значение этого минимума есть .

Следовательно, самая длинная труба, которую мы можем пронести из прихожей в коридор, минуя угол, обладает длиною примерно в

футов.

Дадим точное символьное решение (т.е. решим задачу в общем виде).

> D(L);

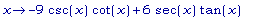
Отсюда следует, что L' = 0 когда

6 sec(x) tan(x) = 9 csc(x) cot(x) или

  = .

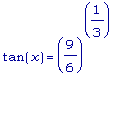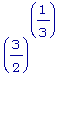Промежутку ( 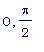) принадлежит единственное значение х, при котором

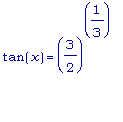
Т.к. 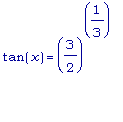, то:

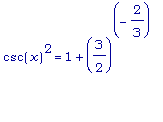и .

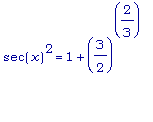> evalf( 9 * sqrt(1 + (3/2)^ (-2/3)) + 6 * sqrt(1 + (3/2) ^(2/3)) );

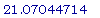
Мы видим, что результаты обоих решений в отношении наибольшей длины трубы совпали.

We need to check that we have a minimum for the function L.

Из выражения для первой производной следует, что L'(x) > 0 , если tan(x) > (3/2)^(1/3),

и L'(x) < 0 , если .

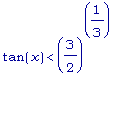Пусть c - единственная точка из промежутка ( 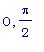), где tan(c) = (3/2)^(1/3).

Из численного решения мы знаем, что c примерно равно

Построим график функции tan(x).

> aa:= plot(tan(x), x = 0 .. Pi/2 - .1, color = black):

> bb:= plot([t,(3/2)^(1/3), t = 0..Pi/2 - .1], color = magenta):

> cc:= textplot([1.1,6,`tan(x)`], color = red):

> dd:= textplot([.5,2.5,`y = (3/2)^(1/3)`], color = red):

> display({aa,bb,cc,dd});

Из приведенного графика мы видим, что L'(x) < 0 для x < c и L'(x) > 0 для x > c;

следовательно L имеет минимум, когда x = c.