| |
|
|
|
Robert M. Corless
Department of Applied Mathematics
University of Western Ontario
London, Canada
|
|
Copyright 2001 by Robert M. Corless
All rights reserved
|
|

|
|
Programming in Maple
|
|
Программирование в Maple
|
|
|
|
|
|
|
|
Data structures
|
|
Структуры данных
|
|
|
|
>
restart; |
|
>
f := 1
+ (x+z)^3 + tan((x+z)^3)*sin(y); |
|

|
|
>
nops(f); |
|

|
|
>
op(1,f); |
|
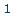
|
|
>
op(2,f); |
|
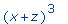
|
|
>
op(3,f); |
|
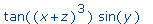
|
|
>
op(1,op(2,f)); |
|
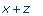
|
|
>
op(1,op(3,f)); |
|
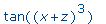
|
|
>
restart; |
|
>
e_seq
:= 1,2,3,4; |
|
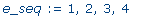
|
|
>
L :=
[1,2,3,4]; |
|
![L := [1, 2, 3, 4]](es.files/03039.gif)
|
|
>
M :=
[4,3,2,1]; |
|
![M := [4, 3, 2, 1]](es.files/030310.gif)
|
|
>
e_seq[3]; |
|

|
|
>
L[3]; |
|

|
|
>
M[3]; |
|

|
|
>
S :=
{1, 2, 3, 4}: |
|
>
T :=
{2, 3, 4, 1}: |
|
>
addressof(S); |
|

|
|
>
addressof(T); |
|

|
|
>
s :=
series( sin(x), x ); |
|
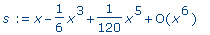
|
|
>
c :=
series( cos(x), x ); |
|
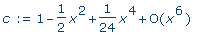
|
|
>
s+c; |
|
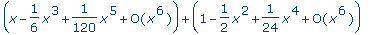
|
|
>
whattype( s+c ); |
|

|
|
>
sumo
:= series( s+c, x ); |
|
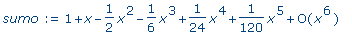
|
|
>
whattype( sumo ); |
|

|
|
>
convert( sumo, polynom ); |
|
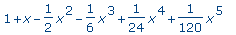
|
|
>
whattype( % ); |
|

|
|
>
series( sin(x^(1/3)), x, 3 ); |
|
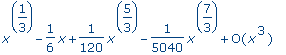
|
|
>
whattype( % ); |
|

|
|
>
lprint( %% ); |
|
x^(1/3)-1/6*x+1/120*x^(5/3)-1/5040*x^(7/3)+O(x^3) |
|
>
series( sin(x), x); |
|
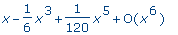
|
|
>
lprint( % ); |
|
series(1*x-1/6*x^3+1/120*x^5+O(x^6),x,6) |
|
>
restart; |
|
>
x; |
|
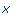
|
|
>
xab12bang_this_is_a_simple_name; |
|
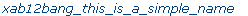
|
|
>
`This
is still a simple name: it just has
weird characters in it@#&*:-)`; |
 |
|
>
restart; |
|
>
x :=
T[3]; |
|
![x := T[3]](es.files/030330.gif)
|
|
>
eval(
T ); |
|

|
|
>
T[5]
:= 7; |
|
![T[5] := 7](es.files/030332.gif)
|
|
>
eval(
T ); |
|
![TABLE([5 = 7])](es.files/030333.gif)
|
|
>
A :=
Matrix( 3, 3, (i,j)->i^(j-1) ); |
|
![A := _rtable[5246512]](es.files/030334.gif)
|
|
>
lprint( A ); |
|
Matrix(3,3,{(1, 1) = 1, (1, 2) = 1,
(1, 3) = 1, (2, 1) = 1, |
|
(2, 2) = 2, (2, 3) = 4, (3, 1) = 1,
(3, 2) = 3, (3, 3) = 9}, |
|
datatype = anything,storage =
rectangular, |
|
order = Fortran_order,shape = []) |
|
>
A[1,2]; |
|
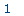
|
|
>
B :=
Vector( 2, i->b[i] ); |
|
![B := _rtable[5114756]](es.files/030336.gif)
|
|
>
C :=
Matrix( 2, 2, (i,j)->c[i,j] ); |
|
![C := _rtable[12879060]](es.files/030337.gif)
|
|
>
adj :=
LinearAlgebra:-Adjoint( C ); |
|
![adj := _rtable[13696836]](es.files/030338.gif)
|
|
>
dt :=
LinearAlgebra:-Determinant( C ); |
|
![dt := c[1,1]*c[2,2]-c[1,2]*c[2,1]](es.files/030339.gif)
|
|
|
|
|
|
|
|
|
С официального разрешения
© 2002 Waterloo Maple, Inc
|
|
|
|
|
|
|

| |
|