| |
|
|
|
Robert M. Corless
Department of Applied Mathematics
University of Western Ontario
London, Canada
|
|
Copyright 2001 by Robert M. Corless
All rights reserved
|
|

|
|
Useful one-word commands
|
|
Использование монокоманд
|
|
|
|
|
|
Solving equations
|
|
Решение уравнений
|
|
|
|
|
|
|
|
dsolve
|
|
Команда
dsolve
|
|
|
|
Fibonacci |
|
>
restart; |
|
>
fib :=
(-4-6*x-6*x^2)*Y(x)+(-1+x+x^2)^2*diff(Y(x),x,x); |
|
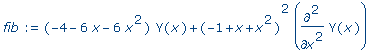
|
|
>
Order
:= 14; |
|
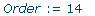
|
|
>
dsolve( {fib,Y(0)=1,D(Y)(0)=1},
Y(x), series ); |
|
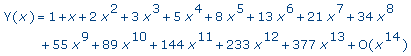
|
|
>
seq(combinat[fibonacci](n),n=1..14); |
|

|
|
>
dsolve( fib, Y(x) ); |
|
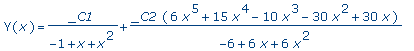
|
|
Combustion |
|
>
de :=
diff(y(x),x) = y(x)^2*(1-y(x)); |
|
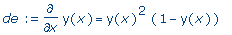
|
|
>
sn :=
dsolve({de,y(0)=10^(-k)},y(x)); |
|
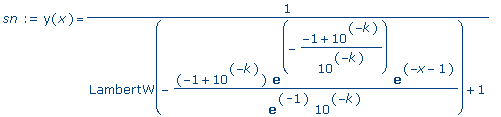
|
|
>
plot3d(rhs(sn),x=0..10^3,k=0..3,axes=BOXED); |
|
![[Maple Plot]](es.files/0202038.gif)
|
|
>
trial
:= eval(sn,k=5); |
|
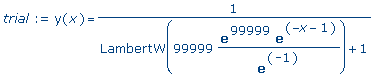
|
|
>
plot(rhs(trial),x=0.999e5..1.001e5); |
|
![[Maple Plot]](es.files/02020310.gif)
|
|
Lotka-Volterra |
|
>
restart; |
|
>
dsys
:= {diff(x(t),t)=x(t)*(1-y(t)),
diff(y(t),t)=s*y(t)*(x(t)-1) }; |
|

|
|
In the text, this line has dsys[1]
and dsys[2] in it; but this violates
one of the "Worksheet Hygiene"
rules, and indeed the dysys set may
be in a different order. So for this
worksheet I have modified the
command to use a substitution to get
it right. This also makes the text
shorter and more intelligible, too. |
|
>
de :=
diff(x(y),y) = subs( x(t)=x(y),
y(t)=y,
subs(dsys,diff(x(t),t)/diff(y(t),t))
); |
|
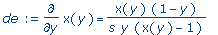
|
|
>
_EnvAllSolutions := true; |
|

|
|
>
dsolve(de,x(y)); |
|
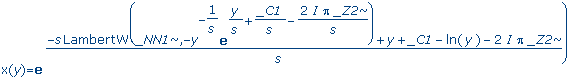
|
|
>
expand(%); |
|
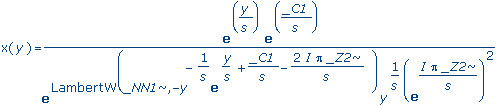
|
|
>
simplify(%); |
|
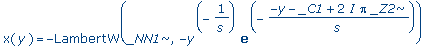
|
|
>
subs(_Z2=0,%); |
|
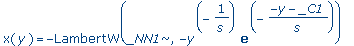
|
|
>
x1 :=
subs(_NN1=0,%); |
|
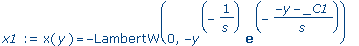
|
|
>
x2 :=
subs(_NN1=-1,%%); |
|
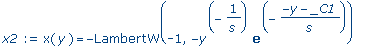
|
|
>
s :=
rand()/1.0e12; |
|

|
|
>
toplot
:=
{[rhs(x1),y,y=0..10],[rhs(x2),y,y=0..10]}; |
|

|
|
>
sols
:=
`union`(seq(toplot,_C1={-7,-6,-5,-4,-3,-2,-3/2,-1-s})): |
|
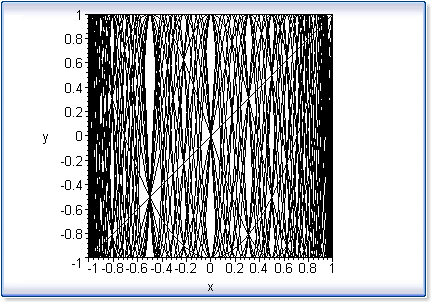
>
plot(%,view=[0..20,0..10],colour=black); |
|
|
|
|
>
eval([x1,x2],y=1); |
|
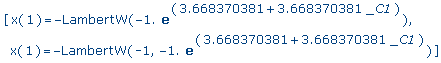
|
|
>
subs(_C1=-1-s,%); |
|
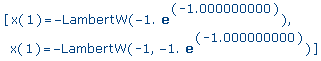
|
|
>
evalf(%); |
|

|
|
>
s :=
's'; |
|

|
|
>
solve(X1 = rhs(eval(x1,y=1)), _C1); |
|
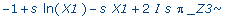
|
|
>
subs(_Z5=0,%); |
|
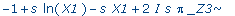
|
|
>
subs(s=0,dsys); |
|
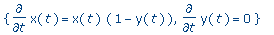
|
|
>
dsolve(%,{x(t),y(t)}); |
|
![[{y(t) = _C2}, {x(t) = _C1*exp(Int(1-y(t),t))}]](es.files/02020331.gif)
|
|
>
dsolve(dsys,{x(t),y(t)}); |
|
![[{x(t) = 0}, {y(t) = _C1*exp(-s*t)}], [{x(t) = Root...](es.files/02020332.gif)
|
|
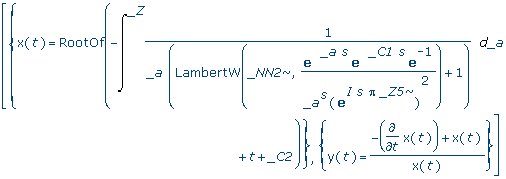
|
|
Airy |
|
>
restart; |
|
>
plots[setoptions](colour=BLACK); |
|
>
AiryDE
:= diff(y(z),z,z) = z*y(z); |
|
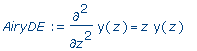
|
|
>
dsolve( AiryDE, y(z) ) ; |
|
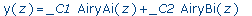
|
|
>
HubbardWest := diff(x(t),t) = x(t)^2
- t; |
|
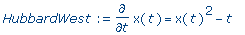
|
|
>
dsolve( HubbardWest, x(t) ); |
|
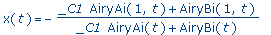
|
|
>
dsolve( {HubbardWest, x(0)=alpha},
x(t) ); |
|
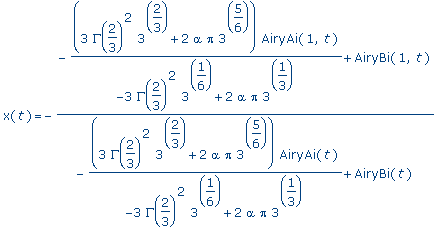
|
|
>
X :=
rhs( % ): |
|
>
Nplot
:= 10; |
|

|
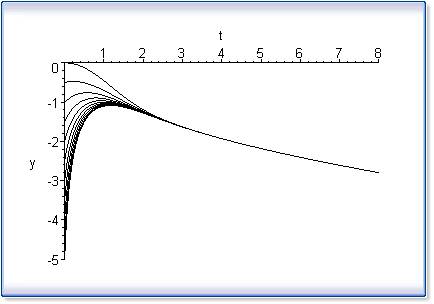
>
P :=
plot( [seq(X,alpha=[seq(-5*i/Nplot,
i=0..Nplot)])],t=0..8, y=-5..0,
scaling=CONSTRAINED ):
plots[display](P); |
|
|
|
|
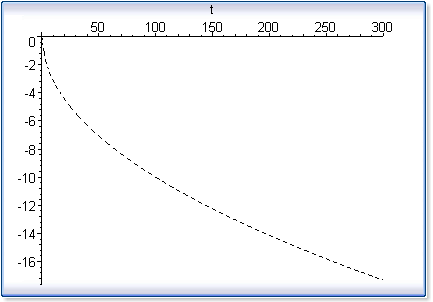
>
P1 :=
plot( eval(X,alpha=0), t=0..300,
linestyle=4 ): plots[display](P1); |
|
|
|
|
>
N :=
3000; |
|

|
|
>
h :=
300.0/N; |
|

|
|
>
badsol
:=
dsolve({HubbardWest,x(0)=0},numeric,method=classical[rk4],
stepsize=h,output=procedurelist); |
|
>
wrongpts := [seq( subs(
badsol(k*h),[t,x(t)]), k=0..N)]: |
|
>
P2 :=
plot( wrongpts, style=POINT,
colour=black, symbol=POINT ): |
|
>
plots[display]({P1,P2}); |
|
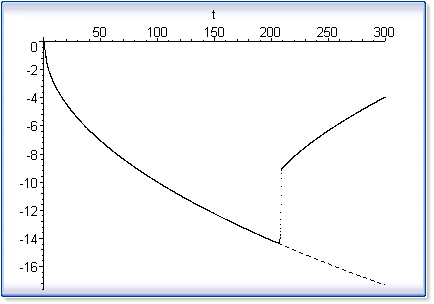
|
|
>
goodsol := dsolve(
{HubbardWest,x(0)=0}, numeric,
stiff=true, range=0..1.0e8 ); |
|

|
|
>
plots[odeplot]( goodsol,
style=POINT, symbol=POINT,
colour=BLACK ); |
|

|
|
>
goodsol( 1.0e5 ); |
|
![[t = .10e6, x(t) = -316.227807972679954]](es.files/02020347.gif)
|
|
>
eval(
X, [alpha=0, t=1.0e5] ); |
|
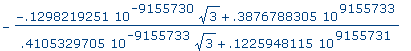
|
|
>
evalf(
% ); |
|

|
|
>
goodsol( 1.0e7 ); |
|
![[t = .10e8, x(t) = -3162.27779889634122]](es.files/02020350.gif)
|
|
>
-sqrt(
1.0e7 ); |
|

|
|
>
eval(
X, [alpha=0, t=1.0e7] ); |
|

|
|
>
goodsol( 1.0e8 ); |
|
![[t = .10e9, x(t) = -9999.9999032634078]](es.files/02020353.gif)
|
|
>
-sqrt(
1.0e8 ); |
|

|
|
Multiple paths from the same
equation |
|
>
restart; |
>
Suzen
:= proc (m, t, yvec, ypvec) local i,
j;
option `[yvec[1] = x(t), yvec[2] =
diff(x(t),t),
yvec[3] = y(t), yvec[4] =
diff(y(t),t)]`;
for i to m/4 do
j := 4*(i-1);
ypvec[1+j] := yvec[2+j];
ypvec[2+j] :=
-yvec[1+j]^2+yvec[3+j]^2;
ypvec[3+j] := yvec[4+j];
ypvec[4+j] := 2*yvec[1+j]*yvec[3+j];
end do;
ypvec
end proc: |
|
>
N :=
72; |
|

|
|
>
ic :=
map(evalf,vector( 4*N,
[seq(op([cos(2*Pi*(i-1)/N),0,sin(2*Pi*(i-1)/N),0]),i=1..N)])): |
|
>
pvars
:= [seq(z||i(t),i=1..4*N)]: |
>
st :=
time(): sol := dsolve( numeric,
procedure=Suzen, range=0..3,
start=0, initial=ic, procvars=pvars
):
time_taken_de := time() - st; |
|
Warning, cannot evaluate the
solution further right of 2.9744778,
probably a singularity |
|

|
>
st :=
time(): plots[odeplot]( sol,
[seq([z||(1+4*(i-1))(t),z||(3+4*(i-1))(t)],i=1..N)],
colour=black, view=[-3..3,-3..3],
scaling=CONSTRAINED, labels=["",""],
axes=BOXED );
time_taken_plotting := time() - st; |
|

|
|
>
time_taken_plotting/time_taken_de; |
|

|
|
|
|
|
|
|
|
|
С официального разрешения
© 2002 Waterloo Maple, Inc
|
|
|
|
|
|
|

| |
|