| |
|
|
|
Robert M. Corless
Department of Applied Mathematics
University of Western Ontario
London, Canada
|
|
Copyright 2001 by Robert M. Corless
All rights reserved
|
|

|
|
Useful one-word commands
|
|
Использование монокоманд
|
|
|
|
|
|
Simplification
|
|
Упрощение
|
|
|
|
|
|
|
|
factor
|
|
Команда
factor
|
|
|
|
>
restart; |
|
>
with(LinearAlgebra): |
|
>
A :=
Matrix( [[-149,-50,-154],
[537,180,546], [-27,-9,-25]] ); |
|
![A := _rtable[18232412]](es.files/0201031.gif)
|
|
>
E :=
Matrix( [[130, -390, 0], [43, -129,
0], [133,-399,0]] ); |
|
![E := _rtable[19443772]](es.files/0201032.gif)
|
|
>
AtE :=
simplify( A + t*E ); |
|
![AtE := _rtable[19445852]](es.files/0201033.gif)
|
|
>
p :=
CharacteristicPolynomial(AtE,x); |
|
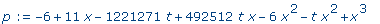
|
|
>
d :=
discrim( p, x ); |
|
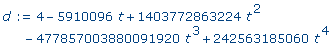
|
|
>
alfs
:= [fsolve( d, t, complex )]; |
|

|
|
>
map(abs,alfs); |
|
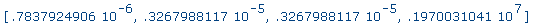
|
|
>
realroot( d, 10^(-14) ); |
|
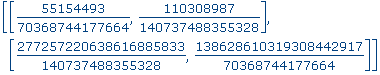
|
|
>
evalf(%); |
|
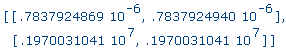
|
|
>
alias(
t[0]=RootOf( d, t ) ); |
|
![t[0]](es.files/02010310.gif)
|
|
>
As :=
eval( AtE, t=t[0] ); |
|
![As := _rtable[19450156]](es.files/02010311.gif)
|
|
>
eigs
:= Eigenvalues( As ); |
|

|
|
>
evalf(
% ); |
|
![_rtable[17838844]](es.files/02010313.gif)
|
|
>
pf :=
eval( p, t=t[0] ); |
|
![pf := -6+11*x-1221271*t[0]+492512*t[0]*x-6*x^2-t[0]...](es.files/02010314.gif)
|
|
>
factor( pf ); |
|

|
|
>
p2 :=
eval( p, t=t/1.0e6 ); |
|
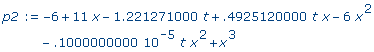
|
|
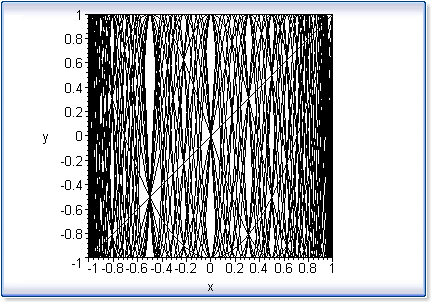
>
algcurves[plot_real_curve]( p2, x,
t, view=[1..3,0..1.0] ); |
|
|
|
>
restart; |
|
>
with(LinearAlgebra): |
>
Yee :=
Matrix( 8,8,
[[1/e, 1/e, 1/e, 1/e, 1/e, 1/e, 1/e,
0],
[1, 1, 1, 1, 1, 1, 0, 1],
[1, 1, 1, 1, 1, 0, 1, 1],
[1, 1, 1, 1, 0, 1, 1, 1],
[1, 1, 1, 0, 1, 1, 1, 1],
[1, 1, 0, 1, 1, 1, 1, 1],
[1, 0, 1, 1, 1, 1, 1, 1],
[0, e, e, e, e, e, e, e]]); |
|
![Yee := _rtable[14284868]](es.files/02010320.gif)
|
|
>
p :=
CharacteristicPolynomial( Yee,
lambda ); |
|
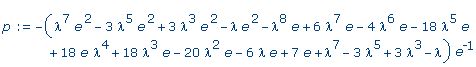
|
|
>
factor(p); |
|
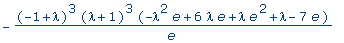
|
|
>
quad_factor := normal(
e*p/(lambda-1)^3/(lambda+1)^3 ); |
|
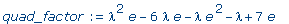
|
|
>
d :=
discrim( quad_factor, lambda ); |
|

|
|
>
factor( d ); |
|
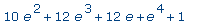
|
|
>
alias(
alpha=RootOf(d,e) ); |
|

|
|
>
pe :=
eval( p, e=alpha ); |
|
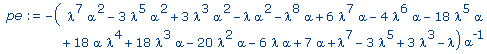
|
|
>
factor( pe ); |
|
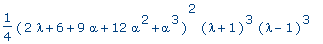
|
|
>
r :=
resultant(quad_factor,lambda-1,lambda); |
|

|
|
>
factor( r ); |
|
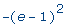
|
|
>
r :=
resultant( quad_factor, lambda+1,
lambda ); |
|

|
|
>
factor( r ); |
|
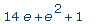
|
|
>
alias(
beta=RootOf(r,e) ); |
|
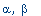
|
|
>
factor( eval(p, e=beta) ); |
|
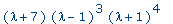
|
|
|
|
|
|
|
|
|
С официального разрешения
© 2002 Waterloo Maple, Inc
|
|
|
|
|
|
|

| |
|