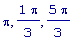>
f7:= x
->cos(x)
+
cos(2*x);
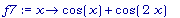
>
plot(f7(x),
x =
0..2*Pi,
color =
black);
![[Maple Plot]](xxx.files/C1-14R36.gif)
>
simplify(
cos(x) +
cos(2*x));
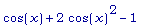
>
factor(%);
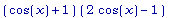
Опять
применили
метод
разложения
левой
части
уравнения
на
множители:
cos(x) =
-1 или 2
cos(x) =
1.
>
plot(cos(x)
+ 1, x =
0..2*Pi,
color =
black);
![[Maple Plot]](xxx.files/C1-14R39.gif)
>
solve(cos(x)
+ 1 =
0,x);

>
plot(2 *
cos(x) -
1, x =
0..2 *
Pi,
color =
black);
![[Maple Plot]](xxx.files/C1-14R41.gif)
>
solve(2
* cos(x)
- 1,x);
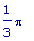
Решения: