>
f := x->8-x^2;
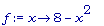
>
a := -2: b := 2:
c := -1: d := 1:
rec1 :=
rectangle([a,
0],[b, f(b)],
color=pink,
thickness=2):
rec2 :=
rectangle([c,
0],[d, f(d)],
color=yellow):
graph :=
plot(f(x),
x=-4..4,
thickness=3):
display(rec1,
rec2, graph);
![[Maple Plot]](xxx.files/C1-0933.gif)
Площадь
прямоугольника
обозначим как AA
. Тогда
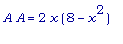 .
.
>
AA:= x -> 2 * x
* ( 8 - x^2);

>
D(AA);

>
solve( 16 - 6 *
x^2= 0,x);
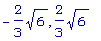
>
evalf(%);

>
D(D(AA))(1.632993162);
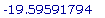
С численной
точки зрения, AA
имеет
критическую
точку x =  ;
т.к. AA''(
;
т.к. AA''(  )
< 0,
)
< 0,
то AA имеет
максимум в точке
x =  .
Т.к.
.
Т.к.
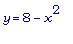 ,
мы имеем
,
мы имеем
y = 8-(  )^2 . Тогда xy
численно есть
)^2 . Тогда xy
численно есть

>
evalf(8 -
(1.632993162)^2);

Точно, AA имеет
максимум когда
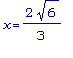 и
и
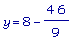 .
.