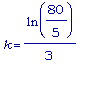Попытаемся составить модель роста или снижения популяции при помощи дифференциального уравнения. Что, если скорость изменения популяции пропорциональна данному количеству y ? Составим и решим соответствующее уравнение для y.

dy/dt = k y .
Разделим переменные:

1*dy/dt/y = d*ln(y)/dt = d/dt*k*t => ln(y) = k*t+C .
Откуда,

y = e^ln(y) = e^(k*t+C) = e^(k*t)*e^C
Положив A = e^C , мы имеем:
y(t) = A*e^kt .
Отметим, что y(0) = A .
ВЫВОД: Решение дифференциального уравнения есть y(t) = y(0)*e^kt

 

Культура бактерий вначале имела численность в 500 шт., а уже через 3 часа насчитывала 8000 шт. (Закон изменения (роста) численности считать экспоненциальным).

a) Найти выражение для числа бактерий через t часов (если с ними не бороться).

b) Найти число бактерий через 4 часа.

c) Когда популяция станет насчитывать 30,000 особей?

d) Построить график выражения части (a)

e) Из графика в (d) попробуйте определить характер изменения популяции со временем?

Из условия следует, что 8000 = 500*e^(3*k) . Определим отсюда k. Имеем::

80/5 = e^(3*k) , откуда ln(80/5) = 3*k . Следовательно, k = ln(80/5)/3 .

 

> k:= ln(80/5)/3;

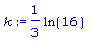
k := 1/3*ln(16)

> evalf(%);

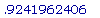
.9241962406

> f1:= t -> 500 * exp(.9241962406 *t);

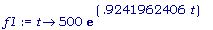
f1 := proc (t) options operator, arrow; 500*exp(.92...

> plot(f1(t), t = 0..5, color = red);

[Maple Plot]

> f1(4);

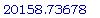
20158.73678

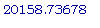
(b) Размер популяции через 4 часа: 20158.73678

> fsolve(500 * exp(.9241962406 *t)= 30000,t);

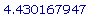
4.430167947

(c) Maple с легкостью определит время t ~ 4.430167947 , через которое численность бактерий достигнет 30,000. Более подробно:

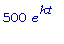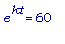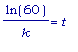30,000 = 500*e^kt => e^kt = 60 => ln(60)/k = t .

Итак, в момент времени 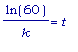ln(60)/k = t численность бактерий равна 30,000.

Напомним, что k примерно равно 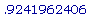.9241962406 . Используя Maple, имеем:

> evalf(ln(60)/ .9241962406);

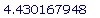
4.430167948

(e) С ростом времени, размер популяции стремится к бесконечности (Почему этого не происходит в жизни?).

 
 
Hosted by uCoz