>
restart:
with(plots):
>
f1:= x -> sin(2
* x) - 2 *
sin(x);
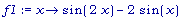
>
plot(f1(x),
x=-Pi- .5..Pi +
.5, color =
red);
![[Maple Plot]](xxx.files/C1-16R4.gif)
>
D(f1);
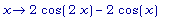
Имеем: f1' (x) = 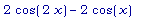
=
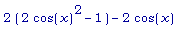
=
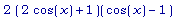
Производная
обращается в 0,
когда cos (x) = 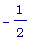 или cos (x) = 1.
или cos (x) = 1.
Построим график
cos (x).
>
plot(cos(x), x=
-Pi..Pi, color =
red);
![[Maple Plot]](xxx.files/C1-16R10.gif)
>
solve(cos(x) =
-1/2, x);
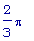
Теперь понятно,
что критическими
точками будут: x
= 0, х =
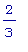
 , и х =
, и х = 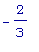
 . Посмотрим на
поведение
производной f1'
(x).
. Посмотрим на
поведение
производной f1'
(x).
Можно заключить,
что f1
возрастает на (
- 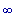 ,
, 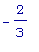
 ) и на (
) и на (
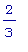
 ,
, 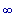 ).
).
Следовательно,
f1 имеет
локальный
максимум в точке
x = 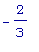
 и локальный
минимум в точке
x =
и локальный
минимум в точке
x = 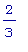

Теперь
разберёмся с
выпуклостью.
>
D(D(f1));
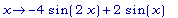
Откуда, f1'' (x)
= -4 sin(2x) +
2sin(x)
= -4(2sin(x)
cos(x))+ 2sin(x)
= 2sin(x)
(-4cos(x) + 1)
Значит, f1'' (x)
= 0 когда sin(x)
= 0 или cos(x) = 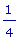 .
.
Т.к.
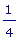 не относится к
известным
значениям
косинуса,
решение
последнего
уравнения
придётся давать
численно.
не относится к
известным
значениям
косинуса,
решение
последнего
уравнения
придётся давать
численно.
>
fsolve(cos(x) =
1/4, x =
-Pi..Pi);
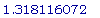
ВЫВОДЫ:
график функции
f1 направлен
выпуклостью вниз
на промежутках ( 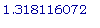 ,0) и (
,0) и ( 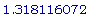 ,
,  ),
),
и выпуклостью
вверх - на
промежутках ( -  ,
, 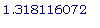 ) и (0,
) и (0, 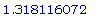 ).
).
Точки перегиба:
x = -  , -
, - 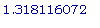 , 0,
, 0, 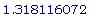 ,
,  .
.
Асимптот нет.