Сообразим картинку для данной ситуации.

> with(plottools):
r := 1: h := 1.2*r:
cyl := cylinder([0,0,-h/2], sqrt(r^2-h^2/4), h, shading=xyz, style=patchnogrid):
ball := sphere([0,0,0], r, color=green):
plots[display]([cyl,ball], scaling=constrained, style=wireframe, orientation=[45,74]);

Пусть r = радиус сферы

a = радиус основания цилиндра

b = 1/2 высоты (т.б. образующей) цилиндра

Мы имеем:

SA = площадь поверхности цилиндра =

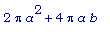
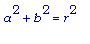(проверьте по рисунку) .

Используя

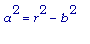
мы получим:

.

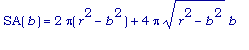Мы хотим найти максимум для SA. При этом мы не ищем лёгких путей! С нами Maple! (И, разумеется, Господь Бог!).

(Объясните намёк, please!)

> assume(r > 0);

> SA:= b ->2* Pi *(r^2 - b^2) + 4 * Pi * sqrt( r^2 - b^2) * b;

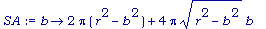
> D(SA);

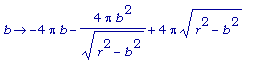
> simplify( -4*Pi*b-4*Pi*b^2/sqrt(r^2-b^2)+4*Pi*sqrt(r^2-b^2) );

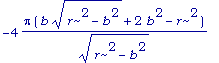
Приравняем числитель нулю и решим получившееся уравнение в отношении b.

> solve( b^2 * ( r^2 - b^2 ) = (r^2 - 2* b^2 )^2, b);

> evalf(%);

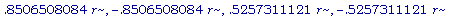
Теперь нам предстоит отсеять все посторонние корни уравнения SA' = 0 и оставить тот, при котором площадь поверхности будет максимальной.

Наличие посторонних корней - ох, как вероятно! Ведь мы возводили обе части уравнения в квадрат! А это действие - не тождественное! Что чревато. Конечно, нас не интересуют отрицательные корни. Хотя бы потому, что сложно найти причину, по которой высота цилиндра станет вдруг отрицательной. Короче, b должно быть положительным.

Проверим, действительно ли SA'( 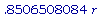) и SA'( 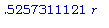) обращаются в 0.

> g:= b -> b*sqrt(r^2-b^2)+2*b^2-r^2;

> g(.8506508084*r);

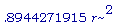
> g(.5257311121*r);

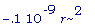
Вывод: SA'( 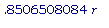) НЕ ЕСТЬ 0, в то время как SA'( 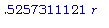) = 0.

Следовательно, единственное критическое значение, которым мы располагаем, есть .

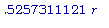Вычислим вторую производную, SA'' , чтобы проверить, имеется ли у функции SA максимум в точке

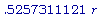
> D(D(SA))(.5257311121*r);

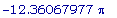
Мы видим, что SA''( 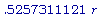) < 0 и, следовательно, SA имеет максимум, когда b = .

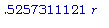> SA(.5257311121*r);

Наибольшая площадь поверхности (в численной форме) : .
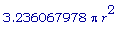